매직 스퀘어, 마방진을 찾아라
페이지 정보
작성자 영재원 댓글 0건 조회 13,241회 작성일 11-06-29 10:59본문
매직 스퀘어, 마방진을 찾아라거장들이 숨겨놓은 그림 속 마방진동서양을 막론하고 ‘마법의 숫자판’으로 불리는 마방진. 이는 신기하게도 상자 속의 숫자를 가로, 세로, 대각선 어느 방향으로 더해도 그 합이 똑같아서 생긴 이름이다. 이는 방진(方陣)·마법진이라고도 하는데, 옛날 사람들은 이에 신비로움을 느껴 때로는 마귀를 쫓는 부적으로도 사용했고, 서양에서는 매직 스퀘어(Magic Square)라 지칭하기도 했다.
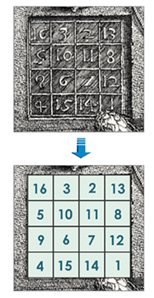
16세기에는 독일 르네상스 시대 최고의 화가이자 동판화가였던 뒤러의 동판화 ‘멜랑꼴리아1’에 마방진이 그려진 것이 계기가 돼 전 유럽에서 유행하게 됐다. 멜랑꼴리아1은 뛰어난 예술성을 갖고 있기도 하지만 마방진과 같은 비밀스럽고 신비로운 내용이 담겨있어 뒤러가 활동하던 시절부터 20세기 초까지 예술학자들의 비상한 관심을 받았다. 멜랑꼴리아1은 1514년에 그려진 동판화로 그림 속의 4방진은 유럽의 방진으로서는 가장 오래된 부류에 속한다. 뒤러는 그림 속 생각에 잠겨 있는 수학자의 뒤에 4방진을 그려 넣었다. 정사각형 모양의 숫자판을 잘 살펴보면 1부터 16까지의 숫자들을 한 번씩 사용해 배열한 것을 볼 수 있다. 특이한 점은 가로줄과 세로줄, 대각선에 배열된 네 수들의 합이 어디에서건 34가 된다는 점이다. 예를 들어 가장 아랫줄 4, 15, 14, 1의 합도 34다. 특히 14와 15는 이 그림의 제작연도인 1415년과 일치해 작가의 숨겨진 의도가 돋보인다. 그렇다면 대각선의 끝에 위치한 숫자들을 살펴보자. 16과 1을 더하면 17이고, 13과 4를 더해도 똑같이 17이 된다. 이와 마찬가지로 안쪽의 작은 정사각형에서 대각선 방향에 있는 숫자인 10과 7, 11과 6의 합도 똑같이 17이다. 이 수들의 합은 어느 것이나 짝수와 홀수의 합인 것. 마방진에 쓰이는 숫자는 중복해서 쓰면 안 되고, 자연수를 꼭 한 번씩만 써야 한다. 이미 완성된 마방진을 보면 간단한 것 같지만 실제로 시도해 보면 숫자를 맞추기가 매우 어렵다. 하지만 많은 사람들이 연구를 거듭한 결과 지금은 매우 큰 수의 마방진까지도 존재한다. 뒤러가 4방진을 등장시킨 이유
‘사성론’은 “인간의 몸 안에는 네 가지 종류의 액체가 흐르고 있는데, 그 중 어느 것이 더 많은지에 따라 그 사람의 성격이 정해진다”는 이론이다. 즉, 혈액이 많은 ‘다혈질’의 사람은 활동가로, 담즙이 많은 ‘담즙질’의 사람은 변덕쟁이로 나뉜다. 또한 점액이 많은 ‘점액질’의 사람은 끈질긴 성격의 사람으로, 흑담즙이 많은 ‘우울질’의 사람은 내성적인 사람으로 분류되는 것. 이러한 사성론에 따라 당시 사람들은 창의적인 사람에 속하는 수학자 등을 우울질의 인간으로 보고, 이들이 건축과 측량, 연금의 신인 토성의 지배를 받는다고 생각했다. 따라서 사색에 열중해 순간 우울질이 높아지게 되면 기분을 전환하기 위해 토성의 영향을 지우고 그 대신 목성의 보조가 필요하다고 생각했다. 당시의 점성술사는 마방진을 별과 연관지어 3방진은 토성, 4방진은 목성, 5방진은 화성, 6방진은 태양, 7방진은 금성, 8방진은 수성, 9방진은 달의 상징이라 했다. 뒤러는 창의적인 사람에 속했던 그림 속 주인공, 수학자가 우울질의 영향에서 벗어나길 바라며 목성을 뜻하는 4방진을 멜랑꼴리아1에 그린 것이다. 씨름도에 숨겨진 마방진의 비밀
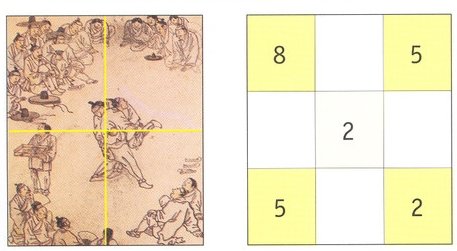
정사각형의 한 변에 배열된 자연수의 개수 n에 방향의 선에 따른 수의 합은 3방진은 15, 4 방진은 34, 5방진은 65, …, n방진은 n(n2+1)/2 이다. 우리나라에도 30세에 진사 시험에 수석 합격하고, 우의정, 좌의정, 대제학을 거쳐 마침내 영의정 등 왕조의 주요 직책을 모두 거쳤던 수학자 최석정(1646∼1715)이 마방진과 유사한 것을 창안해 그의 수학 저서인 ‘구수략(九數略)’에 실었다. 이는 1에서 30까지의 수를 한 번씩만 사용하여 만든 마방진으로, 각 육각형 수의 합은 같다. 서울 광신고 김흥규 수학 교사의 저서 ‘수학 이야기’에 따르면 조선시대 최고의 화가, 김홍도 그림 ‘씨름’에도 마방진의 비밀이 숨어있다. 그림을 살펴보면 중앙에서 씨름을 하는 두 선수를 볼 수 있다. 그런데 이 선수들을 기준으로 가로선과 세로선을 더하기(+) 부호로 그려보면 그림은 네 개의 영역으로 나뉘게 된다. 이렇게 나눠진 네 개의 영역 안에 있는 사람들의 숫자를 세어보면 오른쪽 위 영역은 5, 왼쪽 위 영역은 8, 오른쪽 아래 영역은 2, 왼쪽 아래 영역은 5로 나눠진다. 중간의 씨름 선수 2명을 넣어 대각선에 위치한 세 수들을 더하면 합이 모두 12가 된다. 이 같은 신기한 수의 배열은 ‘X자형 마방진’이라고 부르기도 한다. 이 마방진에는 또 다른 재미있는 숫자의 비밀이 숨어있다. 그것은 가장 윗줄 가로의 합(8+5)과 왼쪽 세로줄의 합(8+5)으로 13이고 가장 아랫쪽 가로줄의 합이 (5+2), 오른쪽 세로줄의 합이 (5+2)로 7이다. 모두 짝수와 홀수의 합으로 이루어진 것이다. 동양에서는 홀수는 하늘과 해를 상징한다고 해서 양(陽)또는 천수(天數)라 불렀다. 또한 짝수는 땅과 달을 상징한다고 해서 음(陰)또는 지수(地數)라 불렀다. 이 수들의 합은 하늘과 땅의 조화는 물론 음양의 조화로 볼 수 있는 것.
구조와 시각 변형으로 최고의 반열에 조선 최고의 화가로 칭해지는 김홍도, 그는 씨름판의 장면을 생동감 있게 선과 색채, 그리고 형태로 구현해 냈다. 그는 그림 중앙의 두 씨름꾼이 온 힘을 다해 한창 시합에 열을 올리며 들배지기로 상대선수를 번쩍 들어 올리는 순간을 포착해 냈다. 김홍도는 이 긴장된 순간의 열기를 한층 더 강조하기 위해 의도적으로 원형 구도를 선택했다. 이러한 원형 구도를 취하면 보는 이로 하여금 저절로 시선이 씨름판 중앙으로 모여지는 효과가 있기 때문이다. 또한 손에 땀을 쥐며 쳐다보는 씨름판 구경꾼들의 긴장을 그대로 전하기 위해 그들이 씨름판을 내려다보는 시점을 취하기도 했다. 이러한 형태와 시각의 변화로 김홍도는 씨름도에서 공격하고 방어하는 두 장사의 엄청난 힘과 씨름판의 열정을 실감나게 전하고 있다. 특히 엿장수 소년은 김홍도의 진가를 보여주기에 충분하다. 익살스런 표정을 짓고 있는 소년은 씨름판의 뜨거운 열기를 뒤로한 채 잠깐 딴청을 부리듯이 먼 곳을 바라보고 있다. 만약 그 소년이 그림에 존재하지 않는다면 어떨까? 화면 중앙으로 쏠려버린 구도 때문에 보는 이들은 답답한 느낌을 갖게 되었을 것이다. 그러나 이 소년의 존재로 그림에 작은 변화가 일면서 그림의 전체적인 답답함이 깨끗이 해소됐다. 단원 김홍도는 마방진까지 응용시킨 구도와 화면의 변형을 자유자재로 다루면서 고유한 화풍까지 유지해 한국 미술역사상 가장 위대한 풍속화가로 평가받고 있다. |
 저작권자 2011.05.19 ⓒ ScienceTimes 저작권자 2011.05.19 ⓒ ScienceTimes |
>본 기사는 ![]() 에서 제공합니다.
에서 제공합니다.
댓글목록
등록된 댓글이 없습니다.

 홈으로
홈으로 로그인
로그인 회원가입
회원가입 사이트맵
사이트맵
 자료실
자료실